Pilots

Memory limit: 64 MB

In the Byteotian Training Centre, the pilots prepare for missions requiring extraordinary precision and control. One measure of a pilot's capability is the duration he is able to fly along a desired route without deviating too much - simply put, whether he can fly steadily. This is not an easy task, as the simulator is so sensitive that it registers even a slightest move of the yoke¹. At each moment the simulator stores a single parameter describing the yoke's position. Before each training session a certain tolerance level is set. The pilots' task then is to fly as long as they can in such a way that all the yoke's position measured during the flight differ by at most 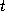. In other words, a fragment of the flight starting at time 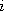and ending at time 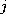is within tolerance level 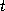if the position measurements, starting with 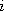-th and ending with 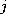-th, form such a sequence 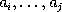that for all elements 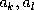of this sequence, the inequality 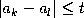holds.

Your task is to write a program that, given a number 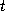and the sequence of yoke's position measurements, determines the length of the longest fragment of the flight that is within the tolerance level .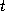

Input

In the first line of the standard input two integers are given, 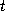and (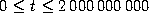, 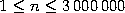), separated by a single space, denoting the tolerance level and the number of yoke's position measurements taken. The second line gives those measurements, separated by single spaces. Each measurement is an integer from the interval from 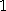to .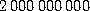

Output

Your program should print a single integer to the standard output: the maximum length of a fragment of the flight that is within the given tolerance level.

Example

For the input data:

3 9
5 1 3 5 8 6 6 9 10

the correct result is:

4

Explanation of the example: There are two longest fragments, both of length 4: 5, 8, 6, 6 and 8, 6, 6, 9.

Task author: Piotr Chrzastowski.